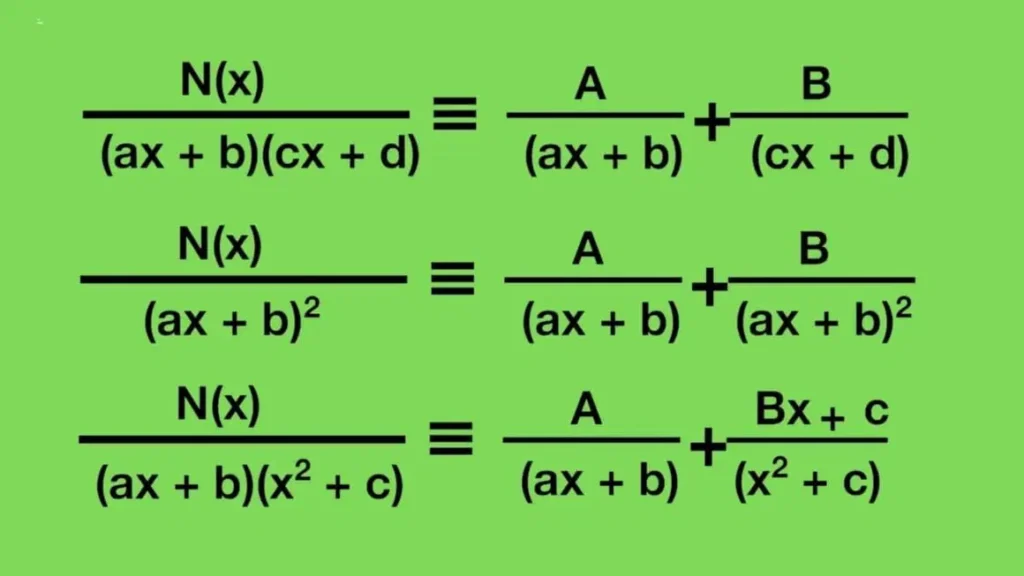Partial Fraction Calculator
Decompose rational functions into simpler fractions
Result
🧮 Partial Fraction Calculator – Simplify Rational Expressions in Seconds
If you’re working with complex rational expressions in algebra or calculus, you’ve probably encountered the need to break them down using partial fraction decomposition. Our Partial Fraction Calculator is a powerful online tool designed to help you instantly simplify these expressions into manageable components, saving you time and reducing errors in your calculations.
Decomposing a rational function into partial fractions is an essential technique in algebra and calculus, especially when dealing with integration or Laplace transforms. Our Partial Fraction Calculator is a free online tool designed to instantly decompose rational expressions into a sum of simpler fractions.
Whether you’re a student, engineer, or math enthusiast, this tool can save you time and effort by delivering accurate solutions with just a few clicks.
🔍 What is Partial Fraction Decomposition?
Partial fraction decomposition is the process of expressing a complex rational expression of the form: P(x)Q(x)\frac{P(x)}{Q(x)}Q(x)P(x)
as a sum of simpler rational expressions whose denominators are factors of Q(x)Q(x)Q(x). This technique is crucial when integrating rational functions or solving differential equations.
Example: 5x+3(x+2)(x−1)=Ax+2+Bx−1\frac{5x + 3}{(x+2)(x-1)} = \frac{A}{x+2} + \frac{B}{x-1}(x+2)(x−1)5x+3=x+2A+x−1B
By solving for constants A and B, we turn a complex expression into an easier form, perfect for integration or analysis.
🧰 Features of Our Partial Fraction Calculator
Our calculator offers more than just answers—it enhances understanding:
✅ Step-by-Step Solutions
Understand how partial fractions are derived with detailed, guided steps.
✅ Supports All Rational Functions
Handles:
- Linear factors
- Repeated factors
- Irreducible quadratic terms
✅ Math Input Simplification
Input expressions easily using standard math notation or copy-paste from math software.
✅ Fast & Free
Get accurate results in milliseconds—no login, no fees.
📘 When and Why to Use a Partial Fraction Calculator
📌 For Integration in Calculus
Integrals of rational functions become manageable with decomposed forms.
📌 For Laplace Transforms
Engineers and scientists use partial fractions to simplify inverse Laplace transforms.
📌 For Learning and Homework
Students gain a better understanding by checking manual work against reliable solutions.
📌 For Automation in Symbolic Computation
Computer algebra systems like MATLAB or Wolfram Alpha use similar methods under the hood.
🧪 Example: Try It Yourself
Input Expression: 3×2+5x+2(x+1)(x−2)(x+3)\frac{3x^2 + 5x + 2}{(x+1)(x-2)(x+3)}(x+1)(x−2)(x+3)3×2+5x+2
Decomposed Output: Ax+1+Bx−2+Cx+3\frac{A}{x+1} + \frac{B}{x-2} + \frac{C}{x+3}x+1A+x−2B+x+3C
Enter this into the calculator and receive:
- The values of A, B, and C
- The decomposed form
- Optional derivation steps
👉 Try the Partial Fraction Calculator Now
🧠 Mathematical Background
Types of Denominators Handled:
- Distinct Linear Factors: 1(x−a)(x−b)=Ax−a+Bx−b\frac{1}{(x-a)(x-b)} = \frac{A}{x-a} + \frac{B}{x-b}(x−a)(x−b)1=x−aA+x−bB
- Repeated Linear Factors: 1(x−a)2=Ax−a+B(x−a)2\frac{1}{(x-a)^2} = \frac{A}{x-a} + \frac{B}{(x-a)^2}(x−a)21=x−aA+(x−a)2B
- Irreducible Quadratic Factors: 1(x2+bx+c)=Ax+Bx2+bx+c\frac{1}{(x^2 + bx + c)} = \frac{Ax + B}{x^2 + bx + c}(x2+bx+c)1=x2+bx+cAx+B
This flexibility makes our calculator suitable for a wide range of academic and professional tasks.
🔗 Related Tools & Learning Resources
Internal Links (on your site):
External Links:
- Paul’s Online Notes – Partial Fractions (DoFollow)
- Khan Academy – Partial Fraction Decomposition (DoFollow)
📊 FAQ – Partial Fraction Calculator
Q1: Can it handle repeated factors and quadratics?
Yes, it supports all standard cases including repeated linear and irreducible quadratic terms.
Q2: Is this tool suitable for integration problems?
Absolutely. Decomposed fractions are ideal for standard integral tables and substitution methods.
Q3: Can I use this on mobile devices?
Yes. The tool is 100% responsive and works across all screen sizes.
🧾 Final Thoughts
The Partial Fraction Calculator is more than just a tool—it’s your shortcut to mastering rational expressions. Whether you’re solving equations, preparing for exams, or exploring advanced math, this tool streamlines the process while enhancing understanding.
Start simplifying your math problems now with our intelligent calculator!
👉 Launch Partial Fraction Calculator